吴春晓 ，黄致新

1.华中师范大学人工智能教育学部，武汉 430079

2.四川省成都市第七中学，成都 610041

3.华中师范大学物理科学与技术学院，武汉 430079

我国的《普通高中物理课程标准（2017年版2020 年修订）》［1］和美国的《下一代科学能力标准》［2］都强调培养学生分析复杂物理问题能力的重要性。与此同时，学生在数学学科中掌握的数学方法要用在物理情境的分析中，仍然需要合适的引导和训练。相反地，如果物理教师简单地认为物理中的数学计算应该全由学生自己解决，而不加引导，那么就会有相当一部分学生由于不熟悉数学分析方法在物理情境中的运用，而产生学习物理的畏难情绪。所以，培养学生在复杂物理问题中进行数学分析的能力，对提升学生的物理学科核心素养很有帮助。

复杂物理情境的分析有难度高、方法多、计算量大等特点，极值问题又是其中对学生科学思维要求很高的一类问题。极值问题在数学中指的就是极大值或者极小值，在物理情境中则对应了在一定条件下某个物理量能够取得的最大值或最小值。在物理情境的表述上经常出现：至少、恰好、刚好、最大、最小、最短、最长等关键词［3］。求解极值问题的方法包括但不限于：利用函数的单调性求极值，利用三角函数求极值，利用二次函数求极值，利用均值不等式求极值，利用图解法求极值［4］。如果仅仅向学生简单地罗列相应的题目和方法，学生只能知道这个题目如何求解，而他们的科学推理能力并没有得到显著提升。只有当学生能够在面临新的物理情境的时候，经由适当的模型建构，能够意识到需要运用这样的方式进行极值的求解，并最终能够得出正确的结论，其科学推理能力才得到了提高。

为了达到培养学生科学思维中科学推理能力这一目标，需要循序渐进地为学生展示在物理情境中均值不等式这一数学工具的使用场景和操作模式。经过了难度螺旋式上升的训练之后，学生才有可能真正掌握均值不等式在物理问题中的使用方法。这样的方法及过程需要从均值不等式的证明开始，在高中物理教学过程中循序渐进地使用，最后学生对在物理情境中运用数学工具才会有更加深刻的感悟。当然，对于其中部分情境而言，可能会有更方便快捷的方法［5］，但是为了不冲淡主题，本文将不再另外展示其他方法。

在数学中，均值不等式又称为平均值不等式、平均不等式，是数学中的一个重要公式。公式内容为调和平均数不超过几何平均数，几何平均数不超过算术平均数，算术平均数不超过平方平均数。关于均值不等式的证明方法有很多，数学归纳法、拉格朗日乘数法、琴生不等式法、排序不等式法、柯西不等式法等，都可以证明均值不等式。物理中运用均值不等式的情境和数学不同，是为了处理实际的物理情境，与此同时，学生在物理情境中需要用均值不等式的时候可能数学学科还没学习均值不等式。不同于高中人教版数学必修5B版［6］中的证明，在物理教学中只需要简单地证明即可：

由于对于任意正数x和y均满足：

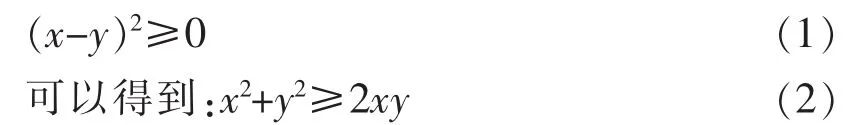
（2）式可以进一步写成如下形式：

在物理中对均值不等式的应用主要是当二者之积为定值时，二者相等时其和可以取得最小值。所以，一个物理问题是否能够运用均值不等式求解的关键往往就在于其表达式的两个部分的乘积是否为定值。

3.1 在运动学中初识均值不等式

学生进入高中的第一步就是学习运动的描述和匀变速直线运动的分析方法，科学思维的培养需要学生体会从模型建构、科学推理、科学论证到质疑与创新这一条完整的分析流程中的每一步。简单地公式套用只能说是科学推理的一部分，通过下面的例1能够在一个简单的物理情境中初步应用均值不等式，给学生展示一个清晰的分析逻辑。

例1已知汽车在加速过程中每秒钟的耗油量与行驶的加速度a的数量关系为Q＝Ma＋N（M、N均为待定量）。若某型号汽车由静止开始做匀加速直线运动，行驶了位移s，若要此段运动中汽车的耗油量最小，则汽车的加速度大小及最小耗油量应为（ ）

解析本题创立了一个对于学生而言比较陌生的情境，所以学生首先需要构建物理模型，也就是需要写出总耗油量Q的表达式。

由于是匀加速直线运动，每秒钟的耗油量恒定，于是得到：

同时，由于汽车做匀加速直线运动，于是：

由此，可以得到t的表达式，代入上式得到：

进一步化简得到：

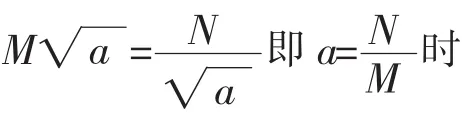
3.2 在重心的确定中拓展均值不等式

在运动学中给学生进行了铺垫之后，进入“重力”这一节时，对于竞赛生，就可以给他们展示例2这样的例子，从而在例1的基础上，再一次加深对均值不等式运用的理解。当然，对于普通高考生而言也完全可以跳过例2，直接在合适的时候给出例3。

例2一个有底无盖的圆柱形桶，底面质量不计，桶侧面质量为a，桶的重心在中轴线上的正中间位置，装满水后水的质量为b。装入水的质量m为多少时，水和桶的合重心最低？

图1 例2示意图

则水和桶的合重心的高度可以表达为：

3.3 在牛顿运动定律中深挖均值不等式

例3如图2所示，粗糙的水平地面上有三块材料完全相同的木块 a、b、c，质量均为 m，b、c 之间用轻质细绳连接。现用一水平恒力F作用在c上，三者开始一起做匀加速运动，运动过程中把一块橡皮泥粘在某一木块上面，系统仍加速运动，且始终没有相对滑动。则在粘上橡皮泥并达到稳定后，下列说法正确的是（ ）

图2 例3示意图

A.无论粘在哪个木块上面，系统的加速度都将减小

B.若粘在a木块上面，绳的拉力减小，a、b间摩擦力不变

C.若粘在a木块上面，绳的拉力增大，a、b间摩擦力增大

D.若粘在c木块上面，绳的拉力和a、b间摩擦力都减小

将质量为m0的橡皮泥粘在a木块上之后，a、b间摩擦力变为：

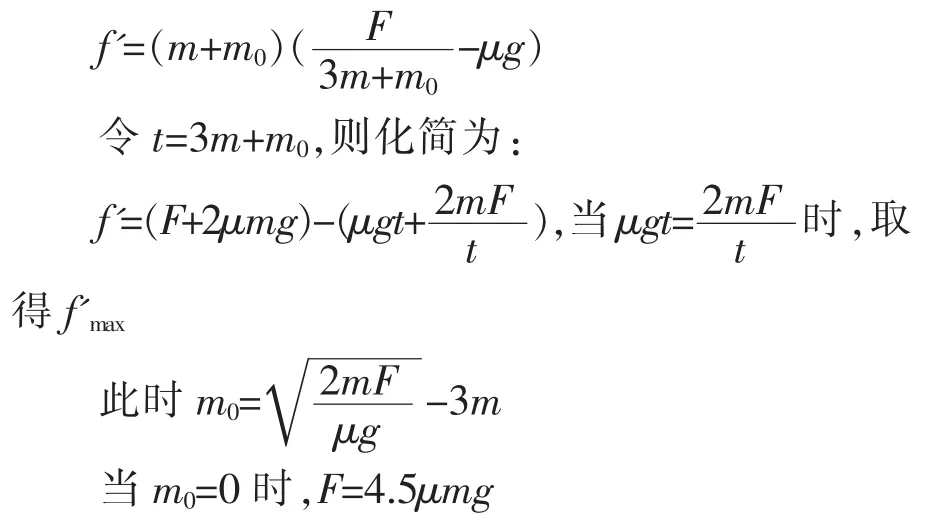
解析本题的正确答案A、D很容易能够选出来，这里不再赘述。为进一步深挖均值不等式的应用，对B选项进行再研究。教师可以将B选项的严格证明作为一个思考题布置给学生，激发他们的探究精神。

由牛顿运动定律可以得到，将质量为m0的橡皮泥粘在a木块上之前，a、b间摩擦力为：

这意味着，若 F＝4.5μmg，即 m0＝0 时，即不粘橡皮泥时，已经有 f′max，再往上面粘橡皮泥，则 a、b 间摩擦力会减小。若 F＜4.5μmg，均值不等式无法取等，所以往a木块上粘橡皮泥，则a、b间摩擦力会减小。若 F＞4.5μmg，当 m0取得一个大于零的值时，能取到f′max，所以逐渐往a木块上粘橡皮泥，则a、b间摩擦力会先增加再减小。所以，B选项错误。

这样的思考题，不仅能培养学生利用均值不等式解决物理问题的能力，还能培养学生的科学探究精神。

3.4 在平抛运动中识别均值不等式

在对平抛运动的物体进行分析时，在竖直面限制问题、水平面限制问题、斜面限制问题、抛物面限制问题、圆弧面限制问题都涉及到极值问题的求解，相关的极值问题已经有文章作出过比较全面的归纳［7］，这里不再重复。此处只列举一例比较有代表性的物理情境。

例4探险队员在探险时遇到一个山沟，山沟的一侧竖直，另一侧的坡面呈抛物线形状。队员从山沟的竖直一侧，以速度v0沿水平方向跳向另一侧坡面。如图3所示，以沟底的O点为原点建立坐标系Oxy。已知，山沟竖直一侧的高度为2h，坡面的抛物线方程为，探险队员的质量为m。人视为质点，忽略空气阻力，重力加速度为g。此人水平跳出的速度为多大时，他落在坡面时的动能最小？动能的最小值为多少？

图3 例4示意图

这个在平抛运动中结合动能定理处理极值的问题，不仅涵盖了函数的思想，还从更加灵活的角度，在配方的情况下运用了均值不等式。通过这个式子，学生对于在物理情境中利用均值不等式解决问题的感悟会更加深刻。

3.5 在万有引力中变换均值不等式

例5设想人类开发月球，不断把月球上的矿藏搬运到地球上，假定经过长时间开采后，地球仍可看作是均匀的球体，月球仍沿开采前的圆周轨道运动，则与开采前相比（ ）

A.地球与月球的万有引力将变大

B.地球与月球的万有引力将变小

C.月球绕地球运动的周期将变长

D.月球绕地球运动的周期将变短

解析正确答案B、D中的D选项很容易判断，这里不再赘述。关键是B选项的处理方式就需要用到均值不等式了：

3.6 在动量守恒中融入均值不等式

例6A球的质量是mA，以某一速度v0沿光滑水平面向静止的B球运动，B球的质量是mB，A与B发生正碰，碰撞过程中机械能不损失，当mA不变，而B球质量取不同值时，下列说法中正确的是（ ）

A.mB＝mA时，碰撞后B球的速度最大

B.mB＝mA时，碰撞后B球的动能最大

C.mB＜mA时，mB越小，碰撞后 B 球速度越大

D.mB＞mA时，mB越大，碰撞后 B 球动量越大

【答案】BCD

由于碰撞过程中系统的动量守恒和能量守恒，能够很快得出碰后B球的速度表达式为：

当mB越小，有vB越大，于是A选项错误，C选项正确。

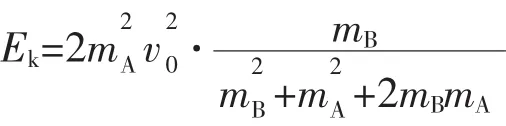
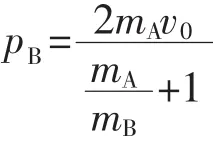
在本情境中，为了化简出均值不等式的形式，采取了分子、分母同除以变量mB的方式，这个方式在不需要采用均值不等式时用于处理分子分母都有变量的表达式也非常便捷。

3.7 在电学实验中活用均值不等式

例7在测定电源电动势和内电阻的实验中，实验室提供了合适的实验器材。某同学误将测量电路连接成如图4所示，其他操作正确，根据电压表的读数U和电流表的读数I，画出U-I图像如图5所示，可得电源的电动势：

图4 例7示意图

图5 U-I图

E＝_______V，内电阻 r＝_______Ω（结果保留两位有效数字）。

解析此题的关键在于R1被分为了两个部分，而这两个部分是并联关系。假设R1左边部分的阻值为x，于是这个并联部分的阻值为：。沿用例5中和定积最大的思想可得，当 x＝R1-x即时，R并取最大值。所以，图 5 中的（0.5 A，2.5 V）这一点就是当滑片在R1中间时测量的值。此时干路电流为电流表示数的两倍，由闭合电路欧姆定律可以得出对应的方程。

由于有两个变量，所以还需要再列一个方程，当滑动变阻器滑片左端阻值为x时的干路电流和当其左端阻值为（R-x）时的干路电流相等，而电流表测量的分别为阻值为x支路的电流和阻值为（R-x）支路的电流。所以，可以等效认为：图5中电压相等的两点对应的电流值分别表示两个支路的电流，其和即为干路电流。于是，从图5中可以找到电压相等的（0.33 A，2.4 V）和（0.87 A，2.4 V）两个点。可以等效为当滑片处于这个位置时，此时并联的两个支路的电流分别为0.33 A和0.87 A，此时的干路电流就是0.33 A+0.87 A=1.2 A，于是由闭合电路欧姆定律可以得到第2个方程。

两个方程联立就可以得出电源电动势大小为 3.0 V，电源内阻大小为 0.50 Ω。

高中物理学科核心素养的培养是一个长期的过程，其中关于数学分析能力的培养也不是简单的一个例题就能一蹴而就的。核心素养真正得到发展的学生一方面能够在不同的物理情境中识别并使用相同的数学方法进行求解，另一方面他们也能在同一个物理情境中运用不同的物理方法进行求解，并比较这些方法。这两个方面分别对应了科学推理方法的纵向培养和不同推理方法的横向对比。本文只专注于同一个科学推理方法在不同物理情境中应用的纵向的培养方式，选取了学生在高中阶段开始接触的均值不等式，这一对他们而言可能还比较陌生的数学工具作为载体，展示了其在高中物理的不同知识板块的应用场景。当然，这些场景可能采取其他的分析方式能够更快地得出结论，但是学生掌握一种工具最好的方式就是反复使用这个工具，熟练使用了之后才能在不同的工具中进行选择。希望通过本文的尝试，能够让更多的学生掌握均值不等式这一工具在物理问题分析中的运用方法，也为他们今后熟练应用其他数学工具提供一点帮助。

猜你喜欢 木块橡皮泥极值 极值点带你去“漂移”新世纪智能(数学备考)(2021年10期)2021-12-21极值点偏移拦路，三法可取河北理科教学研究(2020年3期)2021-01-04极值点偏移问题的解法语数外学习·高中版中旬(2020年10期)2020-09-10怎样数出小木块的个数小学生学习指导(低年级)(2019年9期)2019-09-25一类“极值点偏移”问题的解法与反思中学数学杂志(2019年1期)2019-04-03做个橡皮泥爸爸学生天地(2018年18期)2018-07-05借像皮泥作文周刊·小学一年级版(2016年40期)2017-03-03错在哪里中学生数理化·高一版(2008年11期)2008-06-15