柳成荫，曾 清，龚 毅，乔志浩

（哈尔滨工业大学（深圳）土木与环境工程学院，深圳市土木工程智能结构系统重点实验室，广东 深圳 518055）

传统的桥梁结构健康监测主要是通过在桥梁结构上直接布置传感器，获取并分析其结构响应，从而实现桥梁结构的模态和损伤识别。然而桥梁结构健康系统造价和后期维护成本较为昂贵，在中国交通系统中广泛分布的中小型跨径桥梁上难以大量应用［1］。

为提高桥梁监测的高效性、经济性和移动性，Yang 等［2］最先提出基于过桥车辆响应的桥梁间接监测方法，以移动车辆荷载作为激励，通过对车桥耦合过程中车辆响应的分析，间接提取桥梁的基本频率，由此说明过桥车辆的动力响应中包含桥梁模态参数等相关信息。相比于传统的直接监测，间接监测具备移动性强、无需专门的激励设备等优点。近年来，国内外的学者针对此方法展开了大量研究，成功识别到桥梁结构的固有频率［3］、模态振型［4］、阻尼［5］等重要模态参数，并由此评估桥梁结构的健康状况［6］。

近年来，基于过桥车辆响应的桥梁结构损伤识别研究受到了大量关注［7］。由于振型对于损伤较为敏感，因此大量研究利用其进行桥梁结构损伤识别。Zhang 等［8］提出利用自带敲击装置的过桥小车加速度响应估计桥梁模态振型平方，并通过数值模拟和室内实验验证了使用模态平方识别桥梁损伤的可行性。O’Brien 等［9］提出在过桥小车上安装激光测振仪和加速度传感器，利用小车响应获取较为准确的桥梁振型，再由模态振型平方识别到损伤的存在和位置。He 等［10］通过移动小车的过桥响应获取桥梁的振型曲率，并由此识别损伤的位置。除了振型之外，车桥接触点位置的响应也可用于桥梁的损伤识别。Zhang 等［11］利用车辆接触点响应的瞬时幅值平方进行桥梁损伤识别，数值模拟结果表明该方法能够识别微小损伤的存在。

灵敏度分析的方法也常用于识别桥梁损伤。Bu 等［12］提出利用过桥车辆响应灵敏度识别桥梁损伤，通过正则化和最小二乘法由两自由度小车的车身和车轴加速度反求结构损伤参数，利用数值模拟证明了该方法可以准确识别到桥梁结构损伤的位置和程度。Zhu 等［13］提出利用车桥接触力灵敏度识别桥梁结构损伤，建立了两自由度小车车身振动响应与车桥接触力之间的关系，提出接触力对损伤的灵敏度方程，通过同伦延拓方法由接触力反求桥梁损伤参数，数值模拟结果证明与文献［12］相比，该方法可以提高损伤识别的精度。

可以发现上述基于灵敏度的分析方法基本采用单轴车辆动力学模型，无法反映实际车辆在桥梁上行驶过程中车身竖向和俯仰运动耦合关系。此外，单轴车在实际应用时需要建立拖车系统，适用性有待提高。这些因素均限制了该方法进一步实际应用的可能性。

本文针对四自由度双轴车辆模型，提出了基于车桥接触力灵敏度的桥梁结构损伤识别方法，利用正则化的方法由四自由度车辆接触力反求桥梁损伤参数，实现对桥梁结构损伤位置和程度的识别。文中通过数值模拟算例验证了方法的准确性和有效性，并在此基础上进行详细的参数分析，研究了各个因素独立变化对于结构损伤识别结果的影响，最后针对该方法适用的桥型进行了探讨。

车辆过桥时，车轮与桥面接触点处的竖向作用力称为车桥接触力。考虑车辆行驶过程中车身竖向和俯仰运动的耦合，本文建立双轴四自由度车辆动力学模型及车桥耦合系统，如图1所示。车体构架共有四个自由度，分别是车体浮沉、车体点头及前后车轴浮沉。

图1 车桥耦合模型Fig.1 Vehicle-bridge interaction model

利用达朗贝尔原理，分别对车身和车轴进行分析，建立车辆动力学方程：

式中J为车身转动惯量；
和为车身竖向、俯仰加速度；
和为前后轮竖向加速度；
Fs1，Fs2为车辆悬挂系统的弹性作用力；
Fc1，Fc2为车辆悬挂系统的阻尼力；
Ft1，Ft2为车辆前后轮胎变形带来的弹性作用力：

式中y（xi）和r（xi）分别表示桥梁在接触点位置处xi（i=1，2）的挠度和路面不平度。

用二维四自由度（忽略轴向变形）的梁单元建立简支桥梁模型，根据有限元理论，简支梁结构的振动方程可表示为：

式中Mb，Cb，Kb分别为桥梁的质量、阻尼和刚度矩阵。

桥梁阻尼采用瑞利阻尼，单元阻尼矩阵看作是质量矩阵与刚度矩阵的线性组合：

式中 系数αb，βb与结构的固有频率和阻尼比有关。

桥梁上外力作用由车辆与桥梁间的相互作用力构成：

式中Fb1=Ft1+m1g，Fb2=Ft2+m2g分别为车辆前后轮与桥面接触点处的车桥接触力，其中，m1g和m2g为车辆总重力在前后轮的静态分配，N1（x1），N2（x2）分别为前后轮的整体三次Hermitian 形函数向量［14］。

桥梁在接触点位置处的挠度可由桥梁位移得到：y（xi）=NiT∙yb。前面分别建立了车辆和桥梁两个子系统的模型及运动方程，两个子系统是组成车桥耦合系统的基础，联立方程（1）～（13）得到车桥耦合方程为：

用Newmark 数值分析方法求解运动方程（14）可以得到车辆各部分的加速度响应。车桥接触力是联系车辆和桥梁系统的纽带，体现了车桥系统的耦合性［13］。根据车辆动力学方程，车桥接触力表达式为：

式（23）和（24）表明可以通过车辆的车身竖向加速度、俯仰角及车轴的竖向加速度间接获得车桥接触力。

2.1 接触力灵敏度计算

假定主梁在损伤后仍保持线性弹性和各向同性，本文采用单元抗弯刚度的降低来模拟桥梁结构的损伤。定义损伤参数为α，损伤单元的抗弯刚度可以表示为：

式中 (EI)i为第i号梁单元损伤后的抗弯刚度；
(EI)0i为未发生损伤原始状态的抗弯刚度；
αi为第i号梁单元的抗弯刚度折减系数或损伤参数，其取值范围为0≤αi≤1；
n为总的梁单元数。

利用车桥耦合方程（14）对损伤参数求偏导得到车身、车轴加速度对损伤参数的灵敏度方程：

式（23）对损伤参数求一阶偏导得到接触力对损伤参数的灵敏度：

2.2 桥梁损伤识别

基于响应灵敏度的桥梁损伤识别方法的主要原理为：以车桥耦合模型的计算响应与待测结构实际响应的差值作为输出量，以车桥耦合模型的刚度参数作为输入量，依据响应的差值，逆向调整车桥耦合模型的刚度信息，寻找＜α1，α2，…，αn＞使得响应的差值接近零，此时车桥耦合模型的刚度信息体现的就是实际结构的损伤。计算响应与实际响应的残差δR［15］：

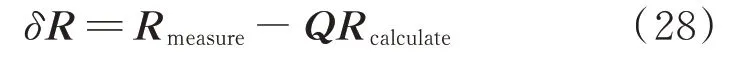
式中Q为使得计算响应与实测响应自由度匹配的选择矩阵；
Rcalculate为车桥耦合模型计算的响应；
Rmeasure为结构实测的响应。

利用式（28）可以获得两种响应的差值，响应具体可以是车身或车轴加速度，本文中更关注的是车辆驶过桥梁时车桥之间的接触力。采用响应灵敏度方法，不考虑二阶和高阶效应，有限元模型的计算接触力在时域上对损伤参数的一阶灵敏度矩阵形式为：

式中Pcal为基于车桥耦合模型计算得到的桥梁刚度损伤参数一阶摄动量；
nt为时间步数，时间步数应大于所求未知量的数目，从而保证方程组是超定的。

损伤参数的一阶摄动量为：

根据惩罚函数理论［16］，可以得到以下关系

式（31）求逆问题经常存在方程病态或者不适定问题，在求解过程中无法得到唯一的真实解。正则化方法是求解不适定反问题的有力工具，利用Tikhonov 正则化方法［17］求得桥梁刚度损伤参数的一阶摄动量为：

式中λ为正则化参数，λ值采用L 曲线法确定［18］；
采用SVD（singular-value decomposition）方法解决其中的伪逆计算［19］。

进一步地可得到桥梁有限元模型迭代一次后，更新的桥梁刚度信息为：

将更新后的桥梁刚度损伤参数回代至车桥耦合有限元模型中继续迭代处理，直至结果符合收敛标准，即有限元模型得到的接触力与待测结构实际的接触力残差接近于零，或者桥梁刚度参数不再变化，此时有限元模型的刚度信息体现的就是实际结构的损伤。

利用车桥接触力灵敏度识别桥梁损伤算法的流程如图2所示。在实际的应用中，车桥接触力也可以通过车辆响应计算得到，具有实际应用的可能性。这里的Tol是很小的收敛临界值，取值量级可选1.0×10−6，根据实际需要可设定合适的收敛标准。同理，后续研究车身、车轴响应灵敏度识别桥梁损伤效果时，只需将流程中的响应及灵敏度替换即可。

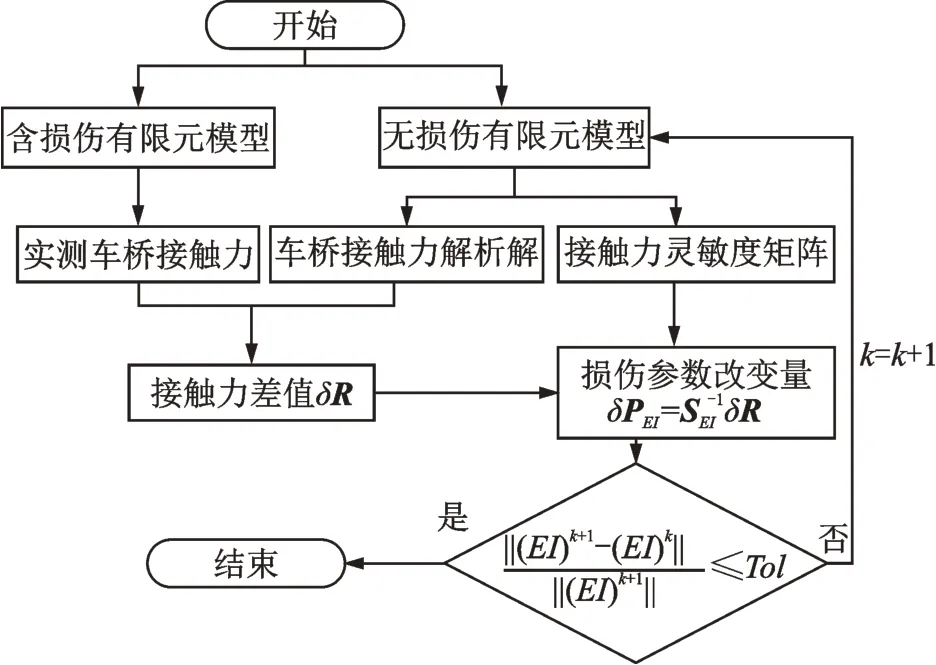
图2 基于车桥接触力灵敏度的损伤识别流程Fig.2 Flowchart of damage detection based on the sensitivity of vehicle-bridge contact force

3.1 车桥耦合模型与损伤工况

为验证基于车桥接触力灵敏度的桥梁损伤识别方法，针对四自由度小车，本文将数值模拟结果与Zhu 等［13］采用两自由度小车进行简支梁桥的损伤识别的结果进行对比。双轴四自由度车辆模型物理参数依据文献［20］进行取值，具体参数如表1所示。简支梁桥模型参数及损伤工况均与文献［13］一致。

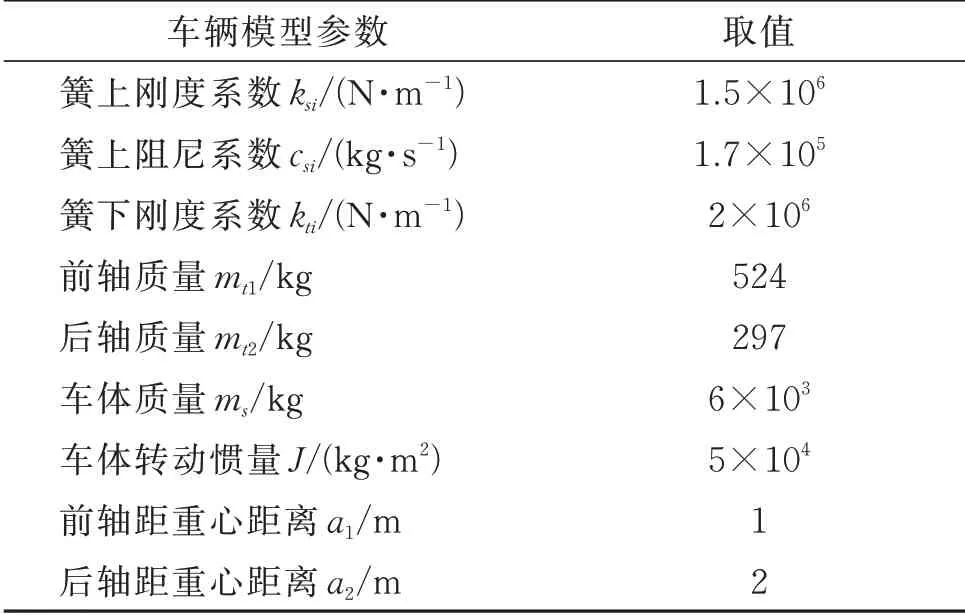
表1 四自由度车辆物理参数（i=1，2）Tab.1 Four degree-of-freedom vehicle physical parame⁃ters（i=1，2）

简支梁桥主要参数如下：计算跨径为30 m，抗弯刚度为2.5×1010N·m2，单位长度质量为6×103kg/m。如图3所示，简支梁桥模型平均分为10 个欧拉梁单元，数据采样频率为200 Hz。车辆过桥速度为20 m/s。路面不平度采用ISO 8608：1995 规范［21］中的C 级。

图3 简支梁桥模型节点编号Fig.3 Nodes of simply supported beam bridge model

桥梁抗弯刚度损伤设置在第1，2，4，6 单元，损伤程度分别为5%，10%，10%，15%。无损伤状态下简支梁桥前3 阶的理论频率分别为：3.6，14.3 和32.1 Hz。桥梁模型采用瑞利阻尼，阻尼系数α和β取值分别为0.343 和0.001。

3.2 简支梁桥损伤识别结果对比

利用上节所述车桥耦合数值模型，可通过采集车辆过桥时车身竖向加速度、俯仰角及车轴的竖向加速度响应，由公式（23）和（24）计算车桥接触力。

本节采用前轴车桥接触力进行损伤识别。识别精度用桥梁所有单元损伤参数的绝对误差AE表示：

式中αreali和αcalculatei分别为第i个梁单元的真实损伤参数和识别损伤参数。本文收敛标准Tol均取1.0×10−6。

由表2可知，在多损伤工况下，四自由度小车的三种响应灵敏度都可以有效识别桥梁刚度损伤的位置及程度。其中，基于接触力灵敏度的损伤识别结果绝对误差仅为0.008%，在识别精度和迭代次数上均优于车身和车轴响应灵敏度，这与文献［13］的结论一致。因此，在考虑路面不平度的工况下，车桥接触力灵敏度能更有效地识别损伤位置及程度。与车辆响应相比，车桥接触力能够包含更多桥梁振动信息。

表2 基于不同响应灵敏度的损伤识别结果（单位：%）Tab.2 Damage detection results based on different response sensitivity（Unit：%）

本文所提出的损伤识别方法对于带损伤的1，2单元的损伤参数识别精确度优于文献［13］，没有识别误差。然而由于支座附近无损伤的第10 单元被误判为出现损伤，使得简支梁的整体损伤参数识别误差高于文献［13］的结果。此外，与文献［13］相比，利用正则化的方法从接触力灵敏度识别结构损伤的方法可以使得迭代次数明显减少（减少78.18%），意味着单元的损伤参数可以较快收敛到真实值。需要指出，同伦延拓方法的迭代次数与同伦参数的取值有关，同伦参数的取值越小，则达到收敛标准的次数也越多，使得最终的迭代次数增加。与文献［12］相比，采用四自由度车辆的接触力灵敏度识别结构损伤可以提高结构损伤识别的精确度（提高88.46%）。通过以上对比可以发现，本文针对四自由度车辆提出的基于车桥接触力灵敏度的结构损伤识别方法可以在保证识别精度的同时显著减少迭代的次数，从而提高损伤识别的效率。

本节分析各项因素对于利用车桥接触力灵敏度识别桥梁损伤的影响，包括车速、车辆质量、频率、数据噪声、建模误差以及桥型。除非特定说明，数值模拟中参数的取值与前文保持一致。

4.1 车辆速度对识别结果的影响

在粗糙路面工况下，车速会影响车桥耦合振动、车桥接触力的大小以及数据的采样点数。车速过快会导致数据采样点过少，进而增大损伤识别误差。本小节主要讨论C 级路面不平度工况下，不同车速对利用接触力灵敏度识别桥梁损伤效果的影响。六种车辆过桥时的常规行驶速度分别为18，36，54，72，90，108 km/h。六种车速工况下基于接触力灵敏度的损伤识别结果如图4所示。

由图4可知，当车辆行驶速度接近54 km/h 时，接触力灵敏度识别桥梁损伤的效果最好，损伤识别的绝对误差约为0.005%。图5为不同车速工况下接触力对4 号梁单元损伤的灵敏度，随着车速增加，接触力的损伤灵敏度不断增大，这有利于提高损伤识别效果。然而，车辆速度同时也会影响数据的采样点数，较高车速下车辆过桥时间偏短，采样点过少，从而导致损伤识别误差增大。综上，为获得较好的桥梁损伤识别效果，车辆过桥速度宜控制在54 km/h 附近。

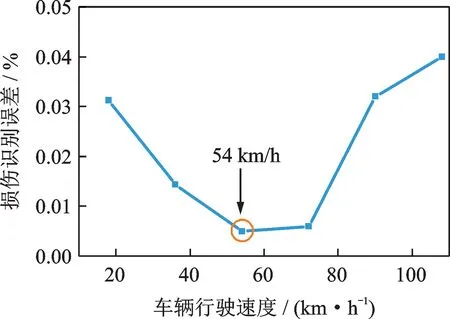
图4 不同车速下损伤识别结果Fig.4 Damage detection results under various speeds

图5 不同车速下接触力灵敏度Fig.5 Sensitivity of contact force under various speeds

4.2 车辆质量和频率对识别结果的影响

过桥车辆的质量和频率会影响接触力识别桥梁损伤的效果，合适的车辆质量能够较好地激发车桥耦合振动。因此，本节主要研究车桥质量比和车桥一阶频率比变化对损伤识别的影响。

在C 级路面不平度工况下，选取车辆行驶速度为54 km/h，车辆质量和频率独立变化。改变汽车质量时，同比例改变车身和车轴的质量；
改变汽车频率时，悬挂系统的刚度参数独立变化。车辆质量和频率变化时，桥梁损伤识别结果如图6和7 所示。

图6表明，车桥质量比为0.03 时，损伤识别的效果最佳，绝对误差为0.003%，而车辆质量过小或过大都会降低损伤识别的效果。图7表明，利用车桥接触力灵敏度识别桥梁损伤存在最优的车桥频率比（约为2.5），该频率比下桥梁损伤识别效果最好，所有单元损伤识别的绝对误差为0.002%，而车辆悬挂系统过柔或过刚都会影响到车身的振动响应进而影响车桥接触力。因此，本文所提出的桥梁损伤识别方法在实际应用时，为获取较好的损伤识别效果，车辆的选择应考虑车桥质量比和一阶频率比的影响。

图6 不同车桥质量比下损伤识别结果Fig.6 Damage detection results under different vehiclebridge mass ratio

图7 不同车桥频率比下损伤识别结果Fig.7 Damage detection results under different vehiclebridge frequency ratios

4.3 数据噪声对识别结果的影响

本文所提出的损伤识别方法需要利用待测结构实际的接触力数据，进而根据有限元模型计算响应和实际响应间的残差来调整有限元模型的刚度信息。因此，数据采集的精度对于损伤识别效果非常重要。然而由于车辆振动的复杂性及传感器精度等原因，采集的车身响应数据往往伴有噪声，本小节通过在接触力中加入不同程度的白噪声模拟被“污染”的测量数据，计算形式为：

式中Pm为模拟实测响应；
Pc为计算响应；
Ep为用百分数表示的噪声水平；
Noise为零均值、单位标准差符合标准正态分布的随机向量；
σ（Pc）为计算响应的标准差。

考虑C 级路面不平度工况下，实际接触力数据包含2%，5%，10%三种不同噪声水平干扰。

接触力数据中的噪声对损伤识别效果影响明显，由图8可见，当实测数据混入2%噪声干扰时，整体识别误差（即AE）为0.7%。随着噪声水平增加，桥梁各单元损伤识别的整体误差明显增加，当实测数据混入10%噪声干扰时，损伤识别整体误差达到2.1%。此外，在不同程度的实测数据噪声影响下，损伤识别的误差主要集中在支座附近的1 号和10 号单元，其原因与车辆在进出桥时产生的桥头跳车现象有关。车辆在刚行驶进或驶出桥梁时的振动响应会明显增大，此时由车身振动响应间接获取的车桥接触力会出现明显波动且识别误差较大，如图9所示，这会降低损伤识别的效果。

图8 不同噪声水平下损伤识别误差分布Fig.8 Damage detection errors under various noise levels

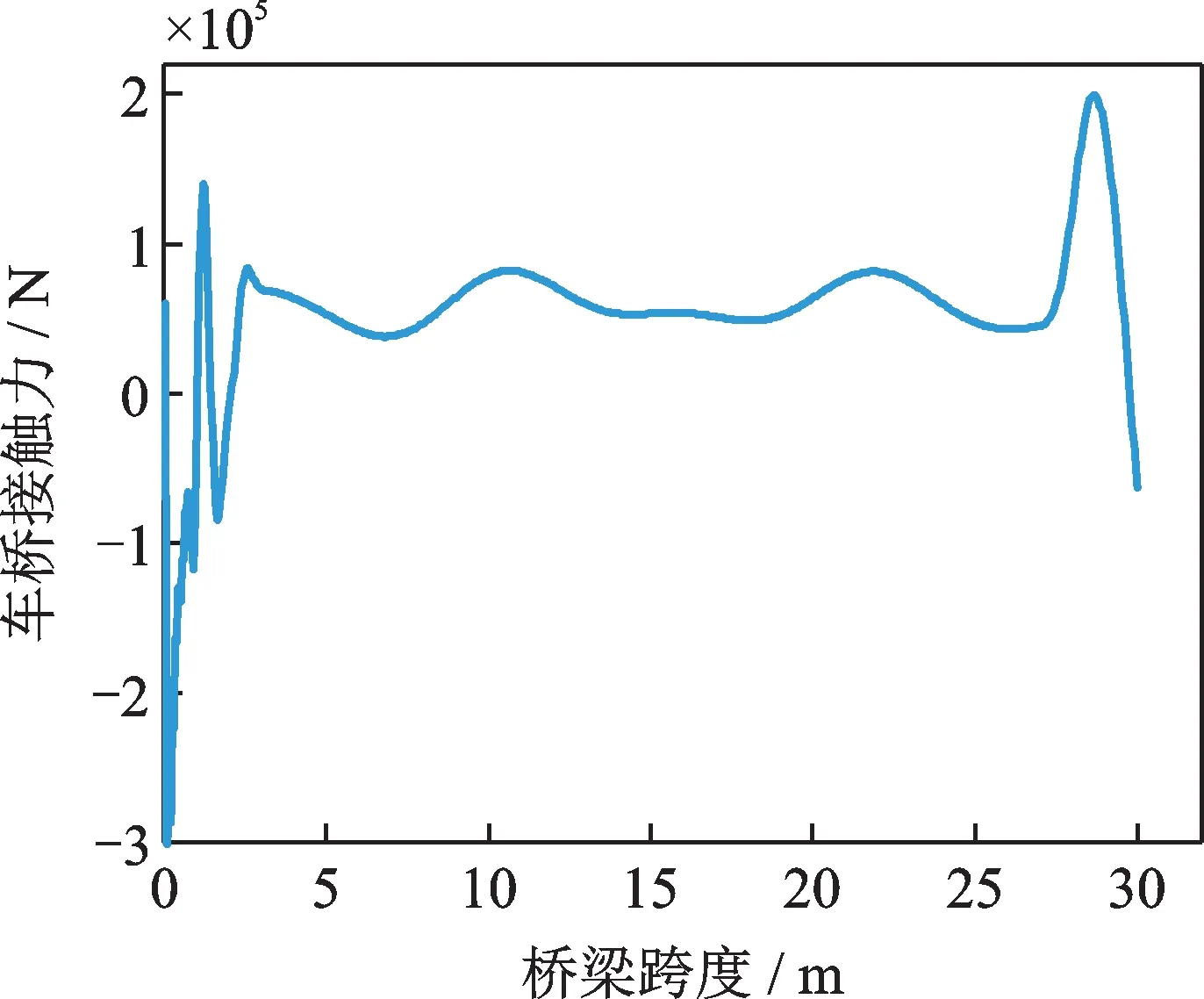
图9 车桥接触力变化图Fig.9 Variation of vehicle-bridge contact force

4.4 桥梁刚度误差对损伤识别结果的影响

本文所提出的损伤识别方法需要依据结构原始资料建立一个有限元基准模型，由于材料特性、建模尺寸、参数选取等各种因素的影响，有限元基准模型难免会产生误差，从而影响损伤识别效果。本节重点研究桥梁基准有限元模型刚度参数误差对于接触力响应识别损伤效果的影响。

根据待测结构的原始资料建立基准有限元模型时，桥梁模型刚度误差分别考虑3%，5%，10%，15%，20%整体刚度折减。用刚度折减后的有限元基准模型作为初始条件进行模型迭代修正和损伤识别，损伤识别结果如图10所示。

图10 不同桥梁模型误差下损伤识别结果Fig.10 Damage detection results under different bridge model errors

数值模拟结果表明，当桥梁刚度误差分别为3%，10%，15%，20%时，模型的整体损伤识别误差均维持在0.3%左右，仍可以通过迭代和调整有限元模型获得接近桥梁真实状态的刚度信息，说明本文提出的基于接触力灵敏度方法的损伤识别算法在模型误差方面具有较强鲁棒性。值得注意的是，当基准桥梁模型的刚度误差为5%时，整体识别误差为0.75%，明显大于其他工况下的损伤识别误差。这是由于基于车桥接触力灵敏度的损伤识别过程是通过迭代调整有限元模型，获取实际响应与计算响应接近时的最优解的过程。当基准有限元模型的迭代初值设置不合理时，尤其是桥梁模型各部分真实损伤的平均值与有限元基准模型整体刚度折减程度接近时，有可能对损伤识别的结果造成一定程度的影响。

4.5 不同桥型对损伤识别结果的影响

本节研究本文提出的基于接触力灵敏度的损伤识别方法对于两跨和三跨连续梁的适用性。

两跨连续梁模型取自文献［13］，主要参数如下：每跨长度为15 m，弹性模量为34 GPa，材料密度为2800 kg/m3，横截面尺寸为4 m×0.25 m，每跨梁均等分为10 个欧拉梁单元。双跨连续梁桥损伤分别设置在第1，6，11，20 单元，损伤程度分别为5%，10%，15%，10%。

三跨连续梁模型如图11所示，每跨长度均为20 m，弹性模量为30 GPa，材料密度为2400 kg/m3，横截面尺寸为1.3 m×0.5 m，每跨梁均等分为10 个欧拉梁单元。三跨连续梁桥损伤分别设置在第1，11，20，30单元，损伤程度分别为10%，5%，5%，10%。

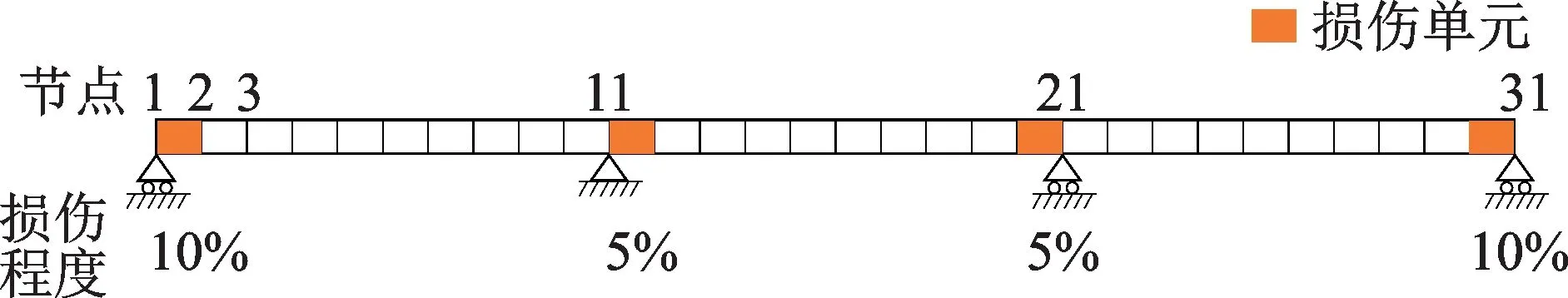
图11 三跨连续梁桥模型节点编号Fig.11 Nodes of three span continuous beam bridge model

根据前文参数分析的结果，四自由度小车车速设为54 km/h，车桥质量比为0.03，车桥频率比为2.5。

图12（a）和（b）中分别给出了无噪声、含5%噪声、含10%噪声三种工况下，利用接触力灵敏度识别两跨和三跨连续梁结构损伤的结果，对于有损伤单元的损伤参数识别结果均精度较高。如表3所示，与简支梁桥的损伤识别结果类似，连续梁损伤识别的误差与迭代次数均随着噪声水平的上升而增加。

图12 连续梁损伤识别结果Fig.12 Damage detection results of continuous beams

表3 连续梁损伤识别绝对误差与迭代次数Tab.3 Damage detection absolute error and iteration number of continuous beams

本文考虑车辆行驶过程中车身竖向和俯仰运动耦合，建立双轴四自由度车辆模型，提出一种基于车桥接触力灵敏度的桥梁损伤识别方法，并探讨路面不平度、车速、车辆质量、噪声、建模误差以及桥型对识别方法的影响，数值模拟结果表明：

（1）在桥梁多损伤工况下，考虑路面不平度影响，接触力灵敏度可以精确识别桥梁损伤的位置及程度，并且识别效果优于车身和车轴响应灵敏度。

（2）利用正则化的方法，从四自由度车辆接触力获取桥梁结构损伤参数，可以在保证一定识别精度的同时明显降低迭代的次数，提高识别的效率。

（3）在过桥车辆选择方面，对于本文的算例而言，存在合适的车桥质量比和一阶频率比使得效果达到最优。

（4）本文提出的基于接触力灵敏度方法的损伤识别算法在桥梁模型刚度误差方面具有较强鲁棒性。

（5）本文提出的损伤识别方法不仅适用于简支梁桥，也适用于两跨和三跨连续梁，均能够较为准确地识别损伤的位置和程度。

（6）数据噪声对损伤识别结果影响较大。此外，由于桥头跳车现象的影响，桥梁支座附近单元的损伤识别存在较大误差，需进一步研究这一现象。

本文仅通过数值模拟对于所提出的损伤识别方法进行验证，未来还将通过室内实验验证该方法的可行性和准确性，包括研究实测车桥接触力的精度等问题。

猜你喜欢车桥灵敏度耦合非Lipschitz条件下超前带跳倒向耦合随机微分方程的Wong-Zakai逼近数学物理学报(2022年2期)2022-04-26车桥剪纸：传统艺术与时代精神的相互融合华人时刊(2022年17期)2022-02-15车桥自动检测校正技术的研究工程与试验(2021年2期)2021-07-14基于磁耦合的高效水下非接触式通信方法研究电子制作(2019年16期)2019-09-27导磁环对LVDT线性度和灵敏度的影响制造技术与机床(2018年12期)2018-12-23地下水非稳定流的灵敏度分析成都信息工程大学学报(2017年1期)2017-07-21基于“壳-固”耦合方法模拟焊接装配大型铸锻件(2015年5期)2015-12-16穿甲爆破弹引信对薄弱目标的灵敏度分析探测与控制学报(2015年4期)2015-12-15基于车桥耦合动力分析的桥梁动应力计算方法中国铁道科学(2015年1期)2015-06-26基于CFD/CSD耦合的叶轮机叶片失速颤振计算航空学报(2015年4期)2015-05-07